心斎橋アートサロンの生徒さん2名が、公募展(旺玄会展)で入選されました。
コロナ禍の中で嬉しいニュースが続きます。
この記事では、そのお二人の出品作品について触れ、黄金比について解説します。
油彩入選作品「望郷」

奈良県吉野町の風景です。
生徒さんご自身が生まれ育った思い入れのある土地を、コロナ禍の中にありながら教室を休むことなく、1年以上に渡って制作されました。
実はこの方、御年88歳!
しかも、今回初めて油絵で50号の大作に挑戦しました。
それだけでも天晴だとは思いませんか。
エネルギーに満ちあふれた方で、今でも1ヵ月に8回スポーツジムに通い、1日に300mを泳ぐそうです。

はっきり言って、僕は負けますね????
油絵を始めたのは、今から約3年半前の2月ですが、それまでは主に水彩画を描いておられました。
水彩画の影響を受け、油絵の具を乗せられるようになるまで時間はかかりましたが、最終的にしっかりと絵の具の乗った、迫力のある風景画に仕上げることができました。
ただ、水面が若干凹んで見えることは問題です。
この点は制作中にも指摘していましたが、出品までに解決することはできませんでした。
問題点は残りましたが、ご本人は今回の制作で様々なものを得ることができたと、大変喜んでおられます。
いつまでも向上心を持ち続けられることには頭が下がりますし、見習わなければなりません。
水彩画入選作品「秋の植物園」

この作品は賞候補となっていましたが、惜しくも受賞を逃してしまいました。
しかし、教室をお休みしながらも、描くことを休まず出品したことは賞賛に値します。
この大作(50F)を制作するにあたっては、以前教室で10号の習作も描いていました。
押さえられた色調ですがしっかりした構図に支えられ、決して大人しくなく凛とした空気感を湛えた良い作品に仕上がっています。
主役となる木の位置がいいですね。
この位置はちょうど黄金比の位置にあたります。
ここで黄金比について解説しておきます。
黄金比の位置の割り出し方
辺AC側を黄金比に分割する場合について説明します。
AC上に中点Pを取り、AP=AQとなる点Qを取ります (図1)。
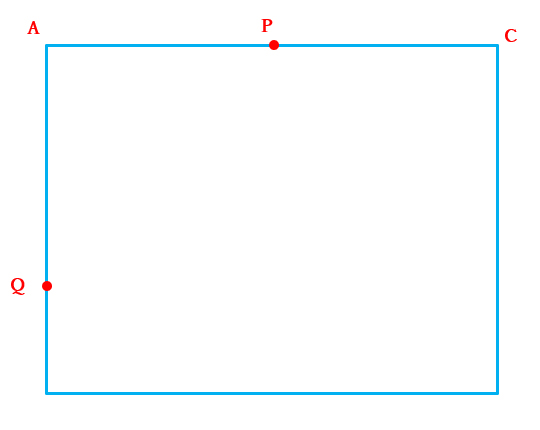
点Cと点Qを結びます (図2)。
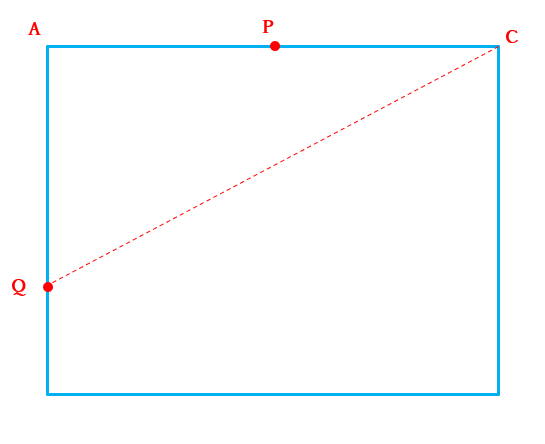
AQ=QRとなる点RをCQ上に取ります (図3)。
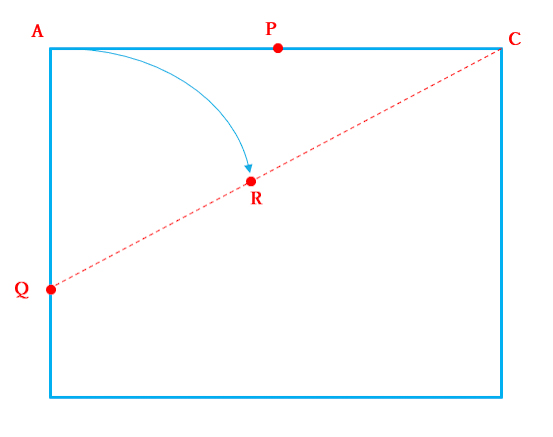
CR=CΦとなる点Φ(ファイ)をAC上に取ると、点Φは辺ACの黄金分割点となります。
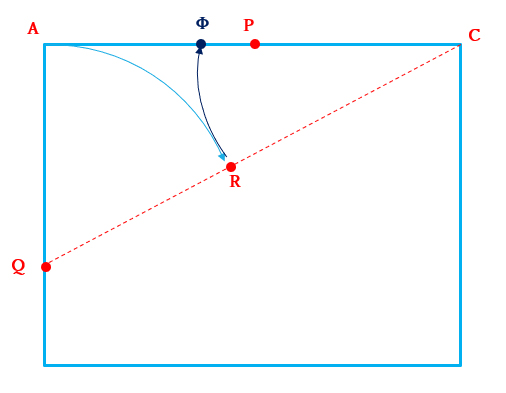
~証明~
△AQCにおいてQA:AC=1:2なので、斜辺CQの長さは三平方の定理より
QA2+AC2=12+22=CQ2
CQ=√5
したがって
CR=√5-1 となるので
AΦ:ΦC={2-(√5-1)}: (√5-1 )
AΦを1とすると
AΦ:ΦC=1:(1+√5)/2
∴ ΦはACの黄金分割点となる。
この図を先ほどの作品に重ねてみます (図5)。

点Φから垂線を下ろすと、主役の木とほぼ重なります。
「ズレてるんじゃないですか?」と仰る方もいるかもしれませんが、多少の誤差は絵画的にはOKです。
この木が同系色の中で主役として強く機能しているのはこのためでもあります。
※ 本人がこれを意識したかどうかは分かりません。
画面には主役が位置するべきポイントがいくつかあるので、黄金比もその一つとして押さえておきたいところです。
✅ 構図の考え方の基本と黄金比については、次の記事でも取り上げているので、興味のある方はご参照ください。
最後に
数学的な話をすると拒絶反応を示す方も少なくないのですが、そういう方は無理に覚えなくてもいいと思います。
構図はあくまでも直感を大事にするべきものですから。
■ 「坂元忠夫の絵画教室」については、以下のリンクをクリックの上、ご参照ください。
遠近法、色彩、人体、構図などの講座ブログは、「絵画講座 / インデックス」として、まとめてありますので、ご活用いただければ幸いです。








コメント