
構図を考える時、画面のどこにモチーフを配置すればいいか分からない。
なんとなくまとまっている気はするけれども、本当にこれでいいのかどうか判断できない、という方は多いのではないでしょうか。
この記事では、構図の考え方の基本を踏まえながら、三分割法について解説します。
三分割法とは

図1は教室でのデモンストレーション作品に、縦、横それぞれ三等分する線を引いたものです。

制作時間は、15分程度です。
いわゆる「三分割法」を利用して、構図を決めています。
この作品の場合、主役となる「橋」を「赤」線上に配置してみました。すべての分割線を使う必要はありません。
この方法は写真の技法書にも頻繁に紹介されており、凡庸な構図ではありますが試してみる価値は十分あります。
決め方も非常にシンプルですし、使いやすいと思います。
構図とは‥ここは最重要です!
図1はF6号サイズですが、おなじ6号でもP6号やM6号のような細長い画面になると、縦横比は変わりますから、この風景にはあてはまりません。
F10号のような正方形に近い形も同様です。
また、「枠」に合わせてモチーフの場所や形を都合よく移動させたり、変形させたりするということでもありません。
手元に10号のキャンバスしかないからといって、余白を無理に空で埋めるようなことはしないのです。

つまり、描きたいモチーフにぴったり合う「枠」を見つけることが、構図の考え方の基本になります。
出来上がった作品に分割線を引いてみて、「ちょうど三等分になっていますね」という解説書を目にすることがありますが、これはちょっと違います。
どの「枠」が適当かを決めるには、何枚もスケッチをするしかありません。
手間を惜しまないことです。
三分割の方法
画面を三等分する際、定規で測りますか。
これってけっこう面倒くさいですよね。
辺の長さを測って、電卓をはじいて…
そんなことをしなくても簡単に三等分を得ることができます。
所詮は絵ですから、図面を引くのとは違います。
だいたい三分の一になればいいので、小さい画面なら手で測ればいいですし、画面が大きくなれば糸などを使っても良いでしょう。
ここでは幾何学的に画面を分割して、三分割を得る方法を紹介します。
まず、対角線を引きます (図2)。
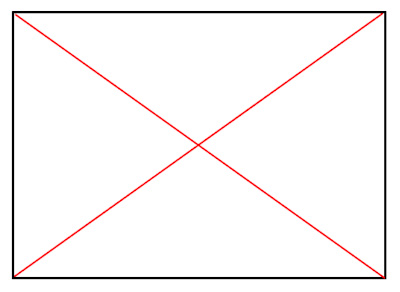
対角線の交点を通る垂直線を引き、画面を二分割します (図3)。
ここでは左右に二分割していますが、上下に二分割しても構いません。
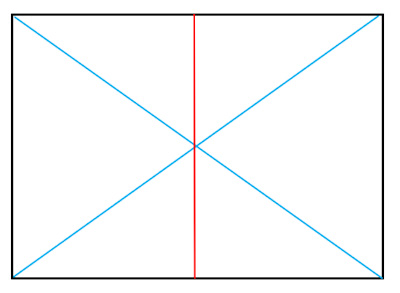
二分割した四角に、それぞれ同じ方向に対角線を引きます (図4)。
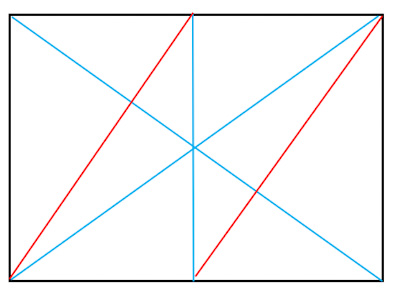
もとの四角の対角線の交点を通るように水平、垂直な線を引けば三分割の線が得られます。(図5)。
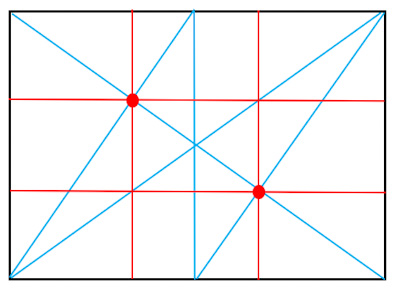
三分割を得るために引いたいくつかの線は、構図を決める上でも重要な線となります。
参考に制作途中のスケッチを載せておきます。

実践編 「構成と構図」
例として、拙作の「ティーポットと果物」をもとに、「構成」と「構図」ついて考えます。

「構図」を考える前に「構成」を考えますが、まずは直感的に並べるところから始めます。
ある程度、納得のいく形になったら、スケッチをして「構図」を検討します。
スケッチに構図線を引いて、画面に対するモチーフの関係をチェックします(図6)。
(構図線は完成作品に引いています)

構成当初、ぶどうはすべて皿の中に納まっていました。

しかし、スケッチに構図線を引いてみると、ぶどうの一部を皿の外に出す方が良いと判断して、構成を変更しています。
写真では見えにくいですが、布の折り目もほぼ分割線の近くに配置してあります。
人の目は三分の一のライン上だと認識しますし、揃いすぎても逆にわざとらしくなってしまいます。
左にあるハート型の小物入れのフタも、構成した当初は閉めていましたが、開けておく方が分割線に響きます。
ハートの形も見せた方が可愛らしいですしね。

「構成」と「構図」は別々に考えるものではない、と理解していただけるのではないでしょうか。
こうやって、より良い形を探りながら調整を繰り返していきます。
✅ ですから、「構成」が出来たら「構図」を考えるということではありません。
三分割法と黄金比との関係
黄金比とは、古代より多くの芸術家や数学者を魅了してきた、最も美しいとされる比率のことです。
「ユークリッド」(前300年頃アレキサンドリアで活躍した数学者)による定義は次の通りです。
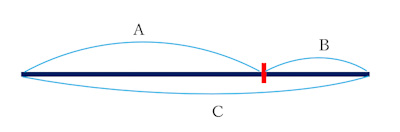
C:A=A:Bとなるような分割比を黄金比といいます。
Bが1の時、Aは(1+√5)/2 、約 1.618となり、これを黄金数Φ(ファイ)と呼びます。
この分割比が活かされた作品は、ミロのヴィーナス、モナリザ、パルテノン神殿など、多数存在しています。
さて、この黄金比と密接な関係にある数列に、「フィボナッチ数列」があります。
これは1、1から始まって、「前の2つの数字を足すと次の数字となる」という単純なルールで作られる数列のことです。
1 1 2 3 5 8 13 21 34 55 89 144・・・・・
名前の由来は、イタリアの数学者「レオナルド・フィボナッチ」(1180~1250頃)からきています。
この数列の隣り合う数字の比を取ると…、
1倍
2倍
1.5倍
1.66666…倍
1.625倍
1.615384…倍
1.61904…倍
1.617647…倍
1.61818182…倍
…というふうに、黄金数Φに収束していくのです。

ここで、3分の1の構図に注目してみます。
分割比は1:2です。
この「1」と「2」という数字は、フィボナッチ数列の第2項目と第3項目にあります。
1 ① ② 3 5 8 13 21 ・・・・・
ここに3分の1の構図と、黄金比との関係があります。
三分割法は単純な分割比による構図法ですが、最も美しい分割比といわれる黄金比から、それほどかけ離れているわけではありません。
大いに活用できる理由はここにあるのです。
巨匠の構図
歴史に残る巨匠たちは、構図についてどのように考えたのでしょうか。
代表的な構図法が見られる作品を取り上げて解説しているので、興味のある方は以下の記事も併せてご覧ください。
最後に
構図を考えるのは非常に難しいですが、〈絵〉の骨となる大事な部分です。
諦めずに何度も調整して、より良い構図を探ってください。
遠近法、色彩、人体、構図などの講座ブログは、「絵画講座 / インデックス」として、まとめてありますので、ご活用いただければ幸いです。








コメント